PS를 위한 컴퓨터 자료구조 강의 1-4강
# 게으른 세그먼트 트리의 구현 # 에 대해 알아보겠습니다.
제목을 보고 드셨을 생각이 뭔지. 잘 압니다.
자료구조가 게으르다고? 뭐지?
저도 똑같은 생각을 했었습니다. 게으른 세그먼트 트리. Lazy Segment Tree에 대해 말씀드리겠습니다.
여기까지 오신 분들은 모두 앞선 연습문제를 풀고 오셨으리라 생각합니다.
아래의 문제를 읽고 오시기 바랍니다.
[구간 합 구하기 - 이전 연습문제]
https://www.acmicpc.net/problem/2042
[구간 합 구하기 2]
https://www.acmicpc.net/problem/10999
무슨 차이가 있는지 느끼셨나요??
넵, 바로 업데이트 함수가 바뀌었습니다.
"idx번 원소를 바꿔라" 가 구간 합 구하기 1의 업데이트였다면
"i번부터 j번까지 모든 원소를 바꿔라"
가 구간 합 구하기2의 업데이트입니다.
이전에 했던 세그먼트 트리처럼 업데이트를 수행하는 경우 i번부터 j번까지 각각 O(logN)의 연산을 수행하므로
구간을 한 번 업데이트 하는데 시간이 O(NlogN)만큼 들게 됩니다.
쿼리의 갯수를 Q라고 한다면 O(QNlogN)으로 절대 시간 내에 돌아갈 수 없습니다.
그렇다면 이 문제를 어떻게 해결해야 할까요?
이 문제를 해결하는 방식이 바로 레이지 세그먼트 트리입니다.
말 그래도 업데이트를 "게으르게" 수행합니다.
다르게 말하면, 업데이트를 "필요한 경우"에만 수행할 수 있도록 하는 겁니다.
이런 생각을 해보면 어떨까요?
1. 최소한의 업데이트를 수행한 뒤, 지금 당장이 아닌, 나중에 업데이트가 필요한 노드에는 징표를 남겨놓는다.
2. 특정 노드에 접근했을 때, 이 노드를 업그레이드 해야한다는 징표가 남아 있으면 업데이트한다.
3. 마지막까지 접근되지 않은, 징표가 있는 노드는 결국 끝까지 업데이트 되지 않는다.
지금 당장은 업데이트하지 않아도, 표식만 남겨놓고 나중에 업데이트할 수 있다면 분명 시간을 줄일 수 있을 것입니다.
레이지 세그먼트 트리는 이런 표식을 심는 연산을 O(logN)에 수행할 수 있습니다.
다시 이전 그림들을 가져오겠습니다.
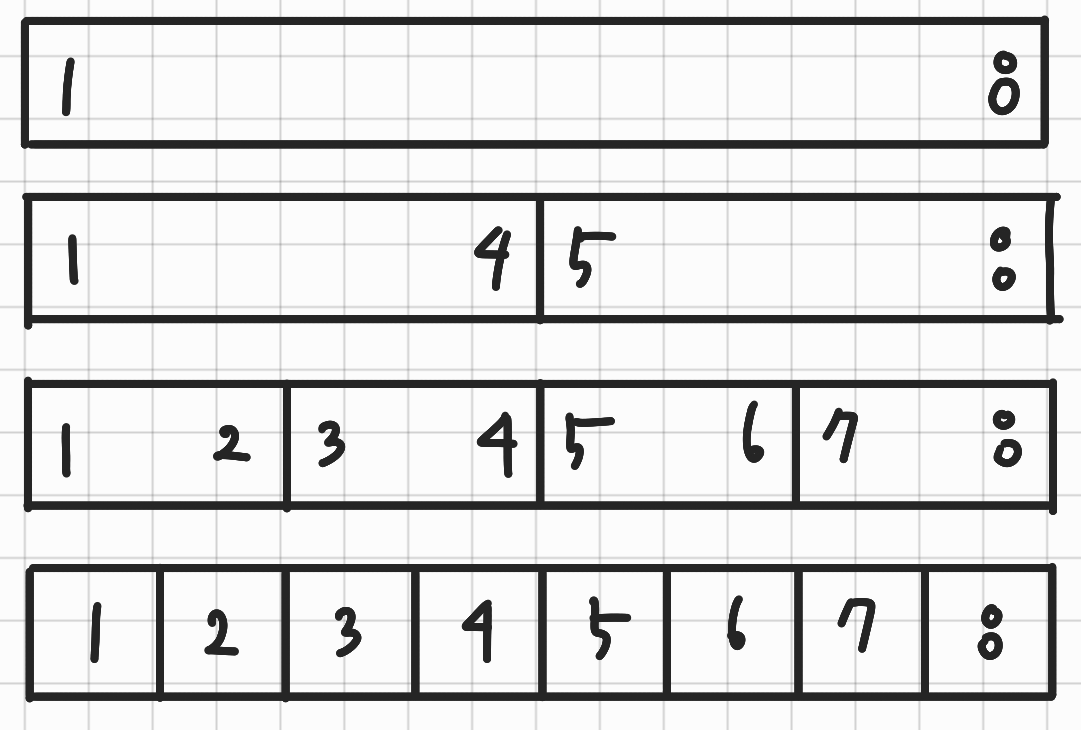
위 배열에서 2부터 8까지의 원소를 1씩 더해주겠습니다.

위에서 색칠된 노드들은 구간의 모든 값이 1씩 더해질 것입니다. 색칠된 [5 8] 노드를 다시 제대로 봅시다.
[5 8] 노드가 더해졌음을 안다면, 그의 자식인 [5 6], [7 8]도 당연히 나중에 더해져야함을 알 수 있습니다.
그렇다면 [5 8]만 업데이트를 완료해놓고, 즉, 구간의 합에 1*4 = 4를 더해놓고,
그들의 자식들에는 표식만 심어놓는건 어떻까요?
표식만 심어놓고 나중에 [5 6]이나 [7 8]노드를 직접적으로 사용해야하는 순간이 오면 그 때 업데이트 하는 겁니다.
[5 6]에 접근했을 때, [5], [6] 노드 역시 업데이트 되어야 함을 알고 있으므로,
[5 6]을 업데이트 한 후, [5], [6] 노드에 표식만 심어놓습니다.
레이지 세그먼트 트리에서는 이 과정을 전파(propagation)라고 합니다.
이제 개념에 대해 어느정도 알게 되었으니 노드를 다음과 같이 설계하겠습니다.
이해를 위해 최적화하지 않는 의사 코드를 이용하겠습니다.
Class 노드:
int 구간의 합
int 왼쪽, 오른쪽
int 징표 = 0 # 초기값은 0
노드 LEFT, RIGHT징표가 새롭게 추가되었음을 볼 수 있습니다.
def 전파(노드 : 노드) -> None:
if 노드.징표 == 0:
return # 징표가 0이라는 뜻은 징표가 없다는 것. 없다면 자기 자신에 업데이트할 것이 없음
노드.구간의 합 += 구간의 원소의 갯수 * 노드.징표
if 자식이 있는 경우:
노드.LEFT.징표 += 노드.징표
노드.RIGHT.징표 += 노드.징표
노드.징표 = 0전파 함수의 핵심은 징표가 있다면 자기 자신을 업데이트 해주고, 자식이 있다면 징표를 물려줍니다.
여기서 자식노드가 이미 징표를 가지고 있을 수도 있으므로, 징표를 바꾸는 것이 아닌 추가를 해주어야합니다.
이제 징표를 심는 업데이트 함수를 만들어주어야합니다.
구간에 완전히 포함되는 가장 큰 노드를 찾는 것.
우리가 이미 많이 해봤죠..!
구간 합 쿼리를 하는 것과 완전히 동일합니다.
따라서 이 연산은 O(logN)에 수행이 가능합니다.
구현에 있어 주의해야할 점이 있습니다.
1. 접근하는 모든 노드는 징표가 있는지 확인하고, 있다면 업데이트 해주어야 한다.
2. 구간에 완전하게 포함되지는 않는 애매한 노드는 업데이트가 완료 되어야한다.
3. 2을 위해서 구간에 완전히 포함되는 노드는 업데이트를 완료하고, 재귀를 끝내고 올라가면서 애매한 노드들 업데이트를 완료해야합니다.
위의 주의점들을 신경쓰면서 설계해보겠습니다.
def 구간 업데이트(노드 : 노드, 추가값 : int, L : int, R : int) -> None:
전파(노드) # 현재 노드에 징표가 있다면 업데이트를 해주어야함.
if 노드.오른쪽 < L or R < 노드.왼쪽:
# 노드에 완전히 포함되지 않는다면 종료
return
if L <= 노드.왼쪽 and 노드.오른쪽 <= R:
# 노드에 완전히 포함
# 자신은 업데이트 해주고, 자식들에게 징표를 심어야함.
노드.징표 += 추가값
전파(노드)
return
중간 = 노드.왼쪽 + 노드.오른쪽 >> 1
구간 업데이트(노드.LEFT, 추가값, L, R)
구간 업데이트(노드.RIGHT, 추가값, L, R)
# 재귀가 끝나면 나 자신의 값을 업데이트 해주어야함.
노드.구간의 합 = 노드.LEFT.구간의 합 + 노드.RIGHT.구간의 합업데이트 함수 설계가 완료되었습니다.
만약 단 하나의 값만 업데이트하고 싶다면, L과 R에 같은 값을 넣어서 업데이트 해도 됩니다만,
약간의 시간 손해가 있습니다.
앞선 값 업데이트 함수에 전파 함수만 추가하면 됩니다.
def 값 업데이트(노드 : 노드, 번호 : int, 추가값 : int):
전파(노드)
if 노드.왼쪽 == 노드.오른쪽:
노드.구간의 합 += 추가값
return
중간 = 노드.왼쪽 + 노드.오른쪽 >> 1
if 번호 <= 중간:
값 업데이트(노드.LEFT, 번호, 추가값)
else:
값 업데이트(노드.RIGHT, 번호, 추가값)
노드.구간의 합 = 노드.LEFT.구간의 합 + 노드.RIGHT.구간의 합
구간 합 쿼리에도 전파 함수만 추가하면 됩니다.
def 쿼리(노드 : 노드, L : int, R : int) -> int :
전파(노드)
if 노드.오른쪽 < L OR R < 노드.왼쪽:
# 완전히 포함되지 않는 노드는 답에 영향을 주지 않기 위해 0을 리턴
return 0
if L <= 노드.왼쪽 AND 노드.오른쪽 <= R:
# 완전히 포함되는 노드는 자신의 값을 리턴
return 노드.구간의 합
중간 = 노드.왼쪽 + 노드.오른쪽 >> 1
# 위 두 조건에 걸리지 않았다면 애매하게 걸쳐 있는 노드, 자식들에게 맡기자.
# 왼쪽 자식이 건져오는 값과 오른쪽 자식이 건져오는 값을 합함
# 만약 포함되는게 없다면 0으로 리턴하여 아무런 영향이 없을것
return 쿼리(노드.LEFT, L, R) + 쿼리(노드.RIGHT, L, R)위 설계 그대로, 배열로서 세그먼트 트리를 구현한 코드를 아래에 첨부합니다.
1. 파이썬
n = (1 << 17) + 2050
class Node:
def __init__(self) -> None:
self.sum = 0
self.lazy = 0 # 징표
tree = [Node()for _ in range(1 << 19)]
def build(arr: list, start: int = 1, end: int = n, node: int = 1) -> None:
if start == end:
tree[node].sum = arr[start-1]
return
mid = start + end >> 1
build(arr, start, mid, node << 1)
build(arr, mid+1, end, node << 1 | 1)
tree[node].sum = tree[node << 1].sum + tree[node << 1 | 1].sum
def propagation(node: int, start: int, end: int) -> None:
if not tree[node].lazy:
return
tree[node].sum += (end - start + 1) * tree[node].lazy
if (start ^ end): # start != end와 동일한 역할의 비트연산
# start != end라는 뜻은 자식 노드가 존재한다는 뜻.
tree[node << 1].lazy += tree[node].lazy
tree[node << 1 | 1].lazy += tree[node].lazy
# 전파 이후에는 징표 삭제
tree[node].lazy = 0
def update_point(idx: int, plus: int, start: int = 1, end: int = n, node: int = 1) -> None:
propagation(node, start, end)
if start == end:
tree[node].sum += plus
return
mid = start + end >> 1
if idx <= mid:
update_point(idx, plus, start, mid, node << 1)
else:
update_point(idx, plus, mid+1, end, node << 1 | 1)
tree[node].sum = tree[node << 1].sum + tree[node << 1 | 1].sum
def update_range(plus: int, l: int, r: int, start: int = 1, end: int = n, node: int = 1) -> None:
propagation(node, start, end)
if end < l or r < start:
return
if l <= start and end <= r:
tree[node].lazy += plus
propagation(node, start, end)
return
mid = start + end >> 1
update_range(plus, l, r, start, mid, node << 1)
update_range(plus, l, r, mid+1, end, node << 1 | 1)
tree[node].sum = tree[node << 1].sum + tree[node << 1 | 1].sum
def query(l: int, r: int, start: int = 1, end: int = n, node: int = 1) -> int:
if end < l or r < start:
return 0
if l <= start and end <= r:
return tree[node].sum
mid = start + end >> 1
return query(l, r, start, mid, node << 1) + query(l, r, mid+1, end, node << 1 | 1)
arr = [*range(1, n+1)]
build(arr)
print(query(2, 5)) # 2+3+4+5
update_range(4, 2, 3) # 2 -> 6, 3 -> 7
print(query(2, 5)) # 6+7+4+52. c++
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int N;
struct Node
{
ll sum, lazy;
Node(){
sum = lazy = 0;
}
};
Node tree[1<<19]; // N보다 큰 가장 작은 2의 제곱수의 2배라 가정 2^19
void build(vector<ll> &arr, int start=1, int end=N, int node=1){
if (start == end){
tree[node].sum = arr[start-1];
return;
}
int mid = start + end >> 1;
build(arr, start, mid, node<<1);
build(arr, mid+1, end, node<<1|1);
tree[node].sum = tree[node<<1].sum + tree[node<<1|1].sum;
}
void propagation(int node, int start, int end){
if (!tree[node].lazy) return;
tree[node].sum += (end - start + 1) * tree[node].lazy;
if (start ^ end){
tree[node<<1].lazy += tree[node].lazy;
tree[node<<1|1].lazy += tree[node].lazy;
}
tree[node].lazy = 0;
}
void update_range(int plus, int l, int r, int start=1, int end=N, int node=1){
propagation(node, start, end);
if (end < l || r < start) return;
if (l <= start && end <= r) {
tree[node].lazy += plus;
propagation(node, start, end);
return;
}
int mid = start + end >> 1;
update_range(plus, l, r, start, mid, node<<1);
update_range(plus, l, r, mid+1, end, node<<1|1);
tree[node].sum = tree[node<<1].sum + tree[node<<1|1].sum;
}
void update_point(int idx, int plus, int start=1, int end=N, int node=1){
propagation(node, start, end);
if (start == end){
tree[node].sum += plus;
return;
}
int mid = start + end >> 1;
if (idx <= mid) update_point(idx, plus, start, mid, node<<1);
else update_point(idx, plus, mid+1, end, node<<1|1);
tree[node].sum = tree[node<<1].sum + tree[node<<1|1].sum;
}
ll query(int l, int r, int start=1, int end=N, int node=1){
propagation(node, start, end);
if (end < l || r < start) return 0;
if (l <= start && end <= r) return tree[node].sum;
int mid = start + end >> 1;
return query(l, r, start, mid, node<<1) + query(l, r, mid+1, end, node<<1|1);
}연습문제 투척합니다.
16975번: 수열과 쿼리 21 (acmicpc.net)
피드백 및 오류 지적은 언제나 환영입니다.
질문은 댓글로 해주셔도 되고, 제 유튜브 채널을 방문해서 하셔도 되고, 오픈채팅방으로 하셔도 됩니다.
[유튜브 : 승욱은] 승욱은 - YouTube
[ 1:1 오픈채팅방] 카카오톡 오픈채팅 (kakao.com)
'알고리즘 설명' 카테고리의 다른 글
| [PS를 위한 자료구조 6강] 세그먼트 트리의 응용 (Orderstatic Tree) (0) | 2022.03.24 |
|---|---|
| [PS를 위한 자료구조 5강] 세그먼트 트리의 구현(비재귀) (0) | 2022.03.24 |
| [PS를 위한 자료구조 3강] 세그먼트 트리의 구현(재귀) 2 (1) | 2022.03.24 |
| [PS를 위한 자료구조 2강] 세그먼트 트리의 구현(재귀) (0) | 2022.03.24 |
| [PS를 위한 자료구조 1강] 세그먼트 트리의 원리와 시간복잡도 (1) | 2022.03.24 |




댓글