PS를 위한 자료구조 1-5강
# 비재귀 세그먼트 트리의 구현 # 에 대해 알아보겠습니다.
지금까지 세그먼트 트리를 모두 재귀 방식으로 구현해왔습니다.
하지만 재귀 호출를 사용하지 않고 세그먼트 트리를 구현할 수 있다니, 믿겨지십니까?
재귀 세그먼트 트리는 비교적 직관적이고 이해가 쉽지만,
비재귀 세그먼트 트리는 이해하기 어렵고 비트연산을 많이 사용해아합니다.
그럼에도 불구하고 왜 비재귀 세그먼트 트리를 사용할까요?
1. 구현이 짧습니다.
2. 동일한 알고리즘 수행의 경우, 함수호출의 횟수가 적은 비재귀가 더 빠릅니다.
3. 그것이 낭만이니까.
웬만해서는 어렵다는 말은 잘 하지 않지만 이번만큼은 조금 어려울 수 있습니다.
그럼 설명을 시작해보겠습니다.
재귀 세그먼트 트리에서는 항상 루트부터 시작했었습니다.
비재귀 세그먼트 트리에서는 반대로 리프노드부터 시작합니다.
리프노드에 어떻게 직접적으로 접근할 수 있을까요?
이를 위해 다시 한번 완전 이진트리를 불러오겠습니다.
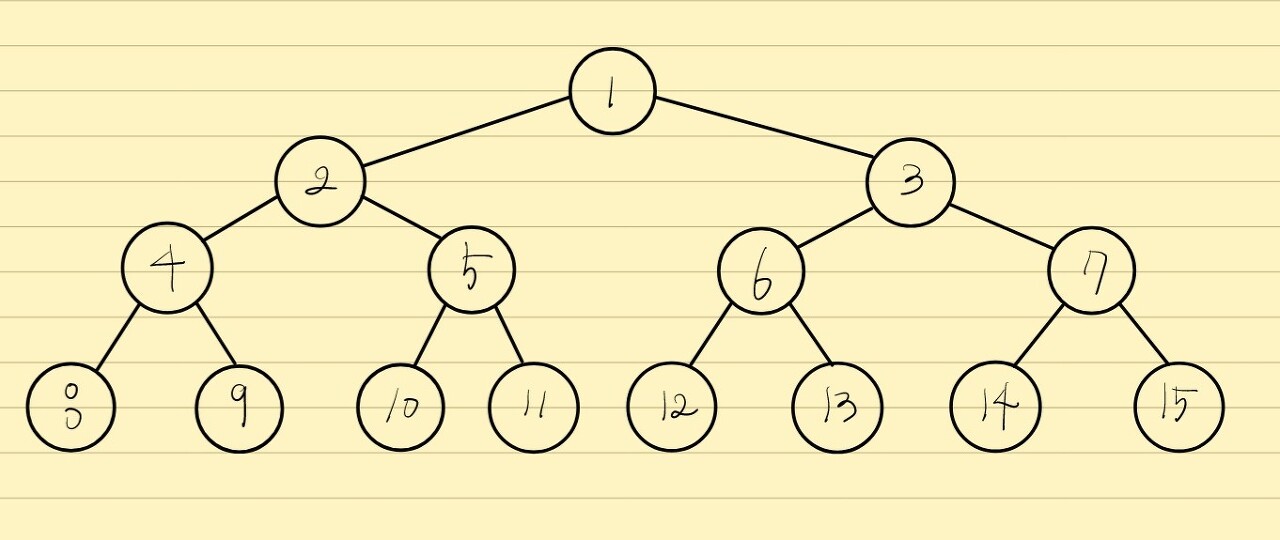
단 이번에는 완전 이진트리 중에서도 "포화 이진트리"를 가져왔습니다.
리프노드가 모두 차있는 트리를 포화 이진트리라고 합니다.
전체 세그먼트 트리의 사이즈는 2^x 꼴입니다.
(노드의 수는 그보다 하나 적지만, 사용하지 않는 0번 노드가 있다고 가정합니다.)
리프노드는 어디부터 시작하나요?
바로 2^(x-1) 입니다. 전체 세그먼트 트리 사이즈의 절반이죠.
리프노드는 2^(x-1)부터 2^x -1까지 총 2^(x-1)개 전체 사이즈의 절반만큼 있음을 알 수 있습니다.
이를 이용해 앞으로 리프노드에 직접적으로 접근할 땐 인덱스에 이 절반의 값을 더해줄 겁니다.
트리를 선언해줍시다.
int 트리[16]배열을 [1,2,3,4,5,6,7,8] 이라고 하면
리프노드에 다음과 같이 등록할 수 있습니다.
for i in 0 to 8:
트리[i+8] = 배열[i]
트리 사이즈의 절반을 더해준 위치에 값을 등록합니다.
단, 여기서 주의해야할 점은, 비재귀 세그먼트 트리는 0-based 인덱스를 가집니다.
지금까지 재귀는 문제풀이의 편의성을 위해 1-based 인덱스로 일부로 바꿨지만,
구현의 편의성을 위해 비재귀에서는 0-based 인덱스로 진행합니다.
이제 트리 전체를 완성시켜주어야 합니다.
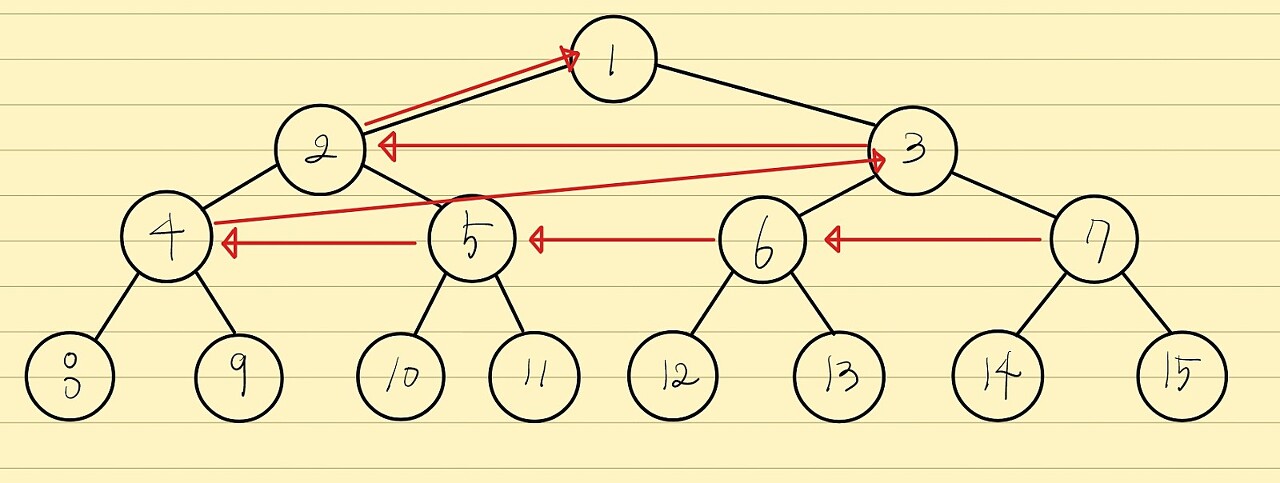
재귀 세그먼트 트리와는 달리 다음과 같은 순서로 트리를 완성시켜주도록 하겠습니다.
절반-1 부터 1까지 반복문을 해주면 되겠죠.
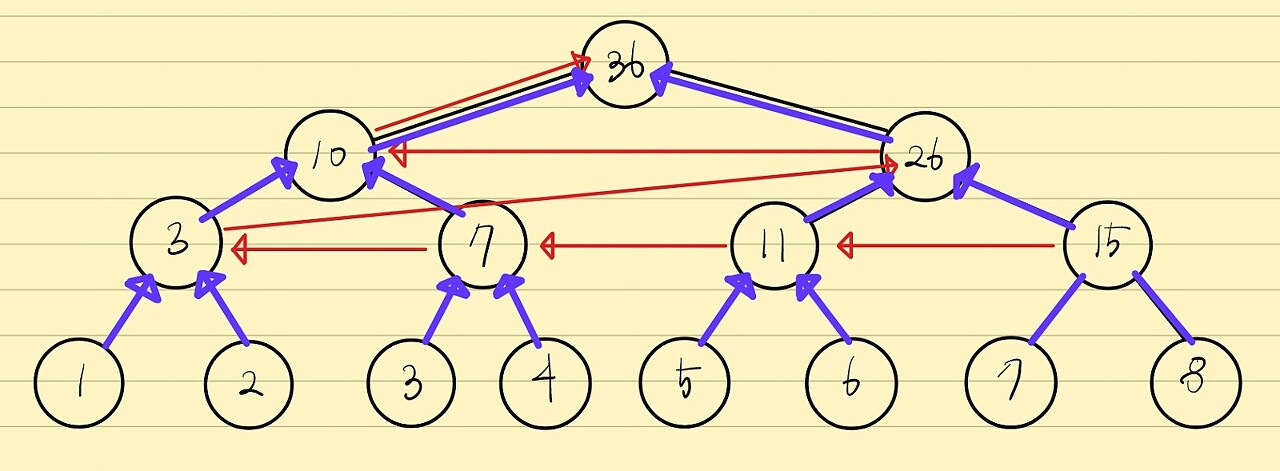
각 노드를 완성시키는 것은 다음과 같이 할 수 있습니다.
트리[노드] = 트리[노드<<1] + 트리[노드<<1|1]
# 두 자식노드의 값을 더해줌.전처리 연산의 의사코드는 다음과 같이 작성할 수 있습니다.
int 트리[사이즈]
int 절반 = 사이즈 >> 1
def 전처리(배열 : list) -> None:
for idx in 0 to 배열의 길이-1:
트리[idx + 절반] = 배열[idx]
# 여기서 "배열의 길이"와 "사이즈"는 다른 변수
for 노드 in 절반-1 to 1:
# 절반-1부터 1까지 반복
트리[노드] = 트리[노드<<1] + 트리[노드<<1|1]
# 모든 트리를 완성주의해야할 점은 루트가 1이기 때문에 1까지만 반복문이 돌아갈 수 있도록 합니다. (0은 사용하지 않습니다.)
이제 값 업데이트 연산을 알아봅시다.
우선 리프노드에 접근해서 해당하는 값을 업데이트 해줍니다.
그리고 부모로 올라가면서 그 값을 업데이트 합니다.
부모로는 어떻게 이동할 수 있을까요?
위 완전 이진트리에서도 볼 수 있듯이, 자신의 번호의 절반이 바로 부모 노드의 번호입니다.
루트 노드에 도달할 때까지 부모로 향합니다.
이를 다음과 같이 구현할 수 있습니다.
def 업데이트(번호 : int, 추가값 : int) -> None:
노드 = 번호 + 절반
트리[노드] += 추가값 # 리프노드에 직접 접근하여 값을 추가함.
while 노드>>1 != 0:
# 부모가 있다면
트리[노드>>1] = 트리[노드] + 트리[노드^1]
# 부모 노드의 값에 없데이트 해줌. 여기서 ^는 xor 연산으로 형제 관계의 노드를 구해줌
노드 >>= 1
# 부모 노드로 접근비트연산이 많고, 이해가 어렵다는 점만 빼면 구현이 짧게 가능하다는 것을 알 수 있습니다.
이제 구간 합 쿼리를 구해보겠습니다.
구간 합 쿼리를 이해하는 것은 극악의 난이도를 자랑합니다.
이를 위해 [3 7] 구간의 구간합을 구하는 과정을 보여드리겠습니다.
0-based 인덱스로 하면 [2 6] 구간임을 주의합시다.
우선 헤당 리프노드에 접근합니다. 여기서는 각각 사이즈의 절반을 더해줘서 2+8=10, 6+8=14 입니다.
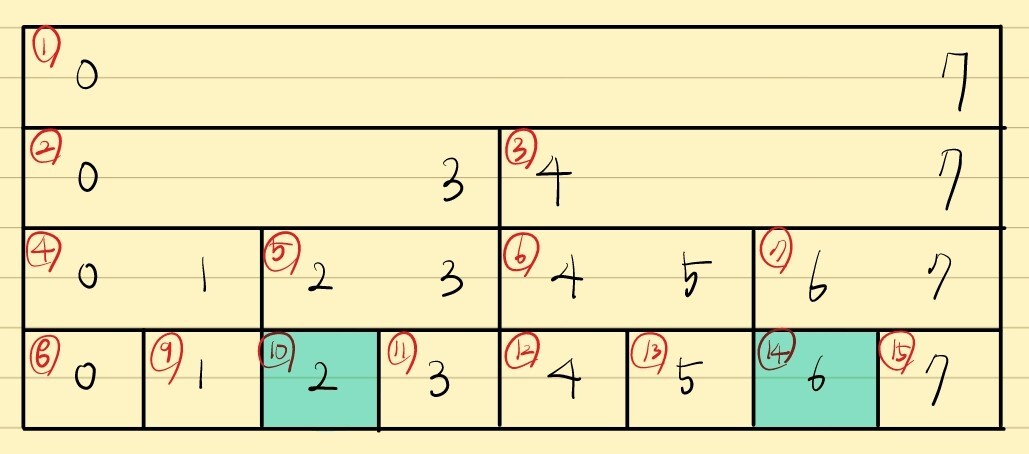
왼쪽 경계를 봅시다.
왼쪽 경계의 노드 번호가 만약 짝수인 경우,
자기 자신을 포함하는 부모 노드도 반드시 구간에 포함됨을 알 수 있습니다.
따라서 이 경우는 부모노드로 올라갑니다.
왼쪽 경계의 노드 번호는 5번이 됩니다.
오른쪽 경계의 노드 번호가 짝수인 경우,
자기 자신을 포함하는 부모 노드가 구간에 절대 포함될 수 없음을 관찰할 수 있습니다.
따라서 이 경우는 해당 노드가 선택 되어야합니다.
그리고 이 노드를 선택함으로써 이 문제는 [2 5] 구간의 문제로 바뀝니다.
따라서 노드의 번호를 1 빼줍니다. 그리고 이 번호는 반드시 홀수입니다.
홀수가 되는 경우 자기 자신을 포함하는 부모 노드가 구간에 반드시 포함됩니다.
따라서 부모로 올라갑니다. 오른쪽 경계의 노드 번호는 6번이 됩니다.
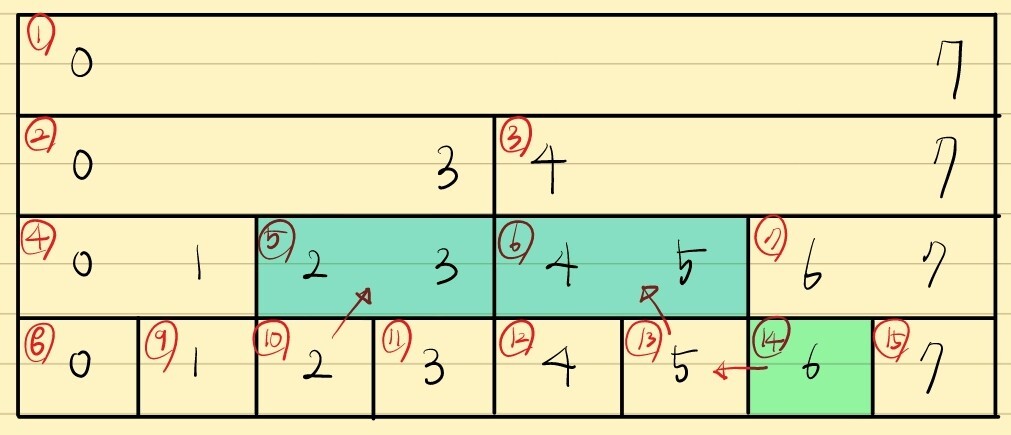
다시 왼쪽 경계를 봅니다.
왼쪽 경계의 노드 번호가 홀수이므로,
자기 자신을 포함하는 부모 노드는 구간에 포함될 수 없습니다.
따라서 해당 노드는 반드시 선택되어야합니다.
그리고 이 구간이 해결됨에 따라 노드 번호를 1 더해줍니다.
그리고 이 번호는 반드시 짝수이므로 부모로 올라갑니다.
따라서 왼쪽 경계의 노드는 3번이 됩니다.
오른쪽 경계는 다시 짝수입니다.
따라서 이 노드를 선택하고 1을 빼준 뒤 부모로 올라가야합니다.
오른쪽 경계의 노드는 2번이 됩니다.
이제 왼쪽 오른쪽 경계의 노드 번호가 교차했으므로 여기서 반복문을 종료합니다.
위의 알고리즘으로 선택한 노드는 다음과 같습니다.
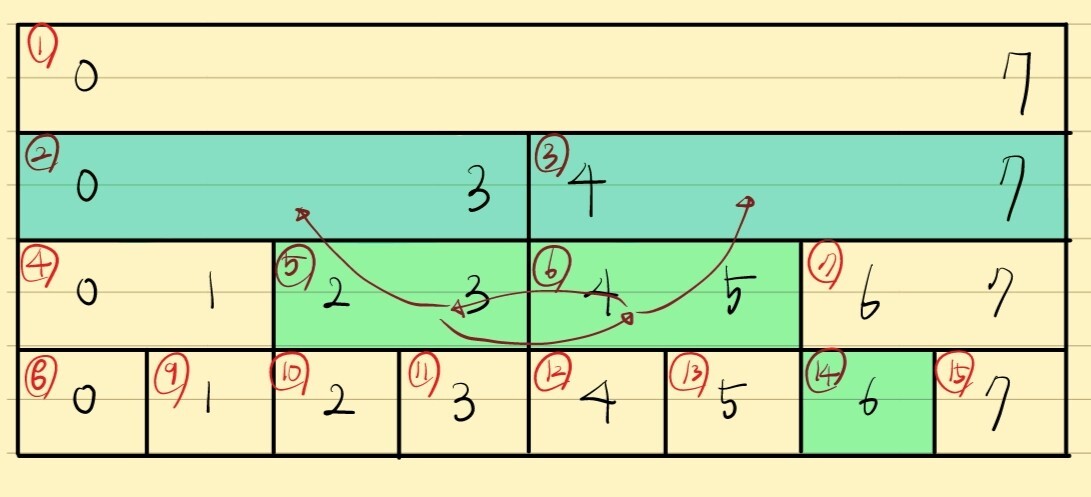
위 알고리즘을 설계하면 다음과 같습니다.
def 구간 합 쿼리(왼쪽 경계 : int, 오른쪽 경계 : int) -> int:
왼쪽 경계 += 절반
오른쪽 경계 += 절반
결과 = 0
while 왼쪽 경계 <= 오른쪽 경계:
# 왼쪽 경계와 오른쪽 경계가 교차하면 종료
if 왼쪽 경계 홀수:
결과 += 트리[왼쪽 경계]
왼쪽 경계 += 1
if 오른쪽 경계 짝수:
결과 += 트리[오른쪽 경계]
오른쪽 경계 -= 1
왼쪽 경계 >>= 1
오른쪽 경계 >>= 1
# 둘 다 부로로 접근
return 결과이해만 하기 어렵지 또 구현 결과는 겁나 간단합니다.
해당 아이디어로 구현한 코드를 첨부합니다.
1. 파이썬
n = (1 << 17) + 2050
tree = [0] * (1 << 19)
HALF = 1 << 18
def build(arr: list) -> None:
for i in range(n):
tree[i+HALF] = arr[i]
for i in range(HALF-1, 0, -1):
tree[i] = tree[i << 1] + tree[i << 1 | 1]
def update(idx: int, plus: int) -> None:
idx += HALF
tree[idx] += plus
while idx >> 1:
tree[idx >> 1] = tree[idx] + tree[idx ^ 1]
idx >>= 1
def query(L: int, R: int) -> int:
L += HALF
R += HALF
ret = 0
while L <= R:
if L & 1:
ret += tree[L]
L += 1
if ~R & 1:
ret += tree[R]
R -= 1
L >>= 1
R >>= 1
return ret
arr = [*range(1, n+1)]
build(arr)
print(query(1, 4)) # 2+3+4+5
update(1, 3) # 3->6
print(query(1, 4)) # 2+6+4+52. C++
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int N;
ll tree[1<<19];
int HALF = 1<<18;
void build(vector<ll> &arr){
for (int i=0; i<N; ++i) tree[i+HALF] = arr[i];
for (int i=HALF-1; i>0; --i) tree[i] = tree[i<<1] + tree[i<<1|1];
}
void update(int idx, ll plus){
idx += HALF;
tree[idx] += plus;
while (idx >>= 1) tree[idx] = tree[idx<<1] + tree[idx<<1|1];
}
ll query(int L, int R){
ll ret = 0;
for (L += HALF, R += HALF; L <= R; L>>=1, R>>=1){
if (L&1) ret += tree[L--];
if (~R&1) ret += tree[R--];
}
return ret;
}레이지 세그먼트 트리도 비재귀 방식으로 구현하는 것이 가능합니다.
자세한 것이 궁금하시다면 아래 링크를 공부해보시면 좋을 것 같습니다.
ruz님 블로그 : 비재귀 lazy propagation 구현 (tistory.com)
메모리를 최적화하는 방법도 있습니다. 단 2*N으로 세그먼트 트리를 구현하는 것이 가능합니다.
아래 링크를 공부해보시면 좋을 것 같습니다.
Efficient and easy segment trees - Codeforces
이번 강의는 연습문제가 딱히 없습니다.
앞선 강의에서 풀어본 문제들을 비재귀로 해결해보세요.
피드백 및 오류 지적은 언제나 환영입니다.
질문은 댓글로 해주셔도 되고, 제 유튜브 채널을 방문해서 하셔도 되고, 오픈채팅방으로 하셔도 됩니다.
[유튜브 : 승욱은] 승욱은 - YouTube
[ 1:1 오픈채팅방] 카카오톡 오픈채팅 (kakao.com)
'알고리즘 설명' 카테고리의 다른 글
| [PS를 위한 자료구조 7강] 세그먼트 트리의 응용 (금광 세그) (2) | 2022.03.24 |
|---|---|
| [PS를 위한 자료구조 6강] 세그먼트 트리의 응용 (Orderstatic Tree) (0) | 2022.03.24 |
| [PS를 위한 자료구조 4강] 게으른 세그먼트 트리의 구현 (0) | 2022.03.24 |
| [PS를 위한 자료구조 3강] 세그먼트 트리의 구현(재귀) 2 (0) | 2022.03.24 |
| [PS를 위한 자료구조 2강] 세그먼트 트리의 구현(재귀) (0) | 2022.03.24 |




댓글