PS를 위한 자료구조 1-6강
# 다양한 세그먼트 트리 테크닉 (Orderstatic Tree) # 에 대해 알아보겠습니다.
Orderstatic tree는 한국말로 딱히 번역이 되어있는 것은 없는 것으로 알고 있습니다.
아래의 문제를 볼까요?
[가운데를 말해요]
https://www.acmicpc.net/problem/1655
이 문제를 어떻게 해결할 수 있을까요?
다음과 같은 자료구조를 생각해봅시다.
(1) 정렬 순서을 유지한채로 삽입하는 것이 O(n)보다 작은 시간복잡도로 가능
(2) 정렬된 자료구조의 특정 인덱스 접근울 O(n)보다 작은 시간복잡도로 가능
언뜻보면 별거 아닐 것 같지만, 절대 평범한 리스트로는 수행할 수 없습니다.
이분탐색으로 삽입할 위치를 O(logN)에 찾을 수 있어도, 삽입 연산은 반드시 O(n)이기 때문이죠.
의외로 이것이 가능한 자료구조는 이진 검색 트리입니다...! 놀랍죠.
이진 검색 트리를 아주 살짝 변형하면, K번째 원소에 접근하는 것이 가능합니다.
그리고 삽입, 삭제, 접근이 모두 O(logN)에 수행하는 것이 가능합니다.
이런 이진 검색 트리의 변형을 Orderstatic Tree라고 합니다.
하지만 이진 검색 트리에는 치명적인 단점이 있습니다.
한쪽으로 치우친 이진 검색 트리는 모든 연산이 O(n)이 되어버리기 때문이죠.
이를 개선하기 위해, 좌우 균형을 맞춘 AVL트리, RedBlack트리, Splay트리 같은 것이 존재하지만,
이들의 구현 난이도는 각각 최종 보스급입니다.
이진 검색 트리보다는 메모리 효율이 낮지만,
세그먼트 트리도 이러한 Orderstatic tree의 역할이 가능합니다..!
다음과 같은 발상을 해보겠습니다.
우리는 지금까지, N개의 자료구조가 있다면 1부터 N까지 범위로 세그먼트 트리를 만들어왔습니다.
이번에는 자료의 범위로 세그먼트 트리를 구성해보겠습니다.
1부터 8까지로 트리의 범위를 제한해보겠습니다.
그리고 각 노드는 담당 구간에 몇 개의 원소가 있는지 저장합니다.
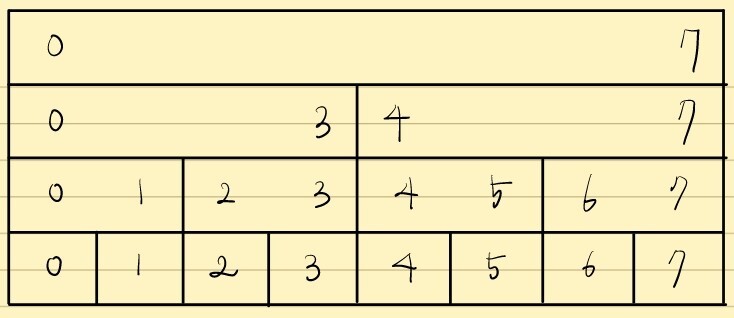
여기에 3을 넣겠습니다.
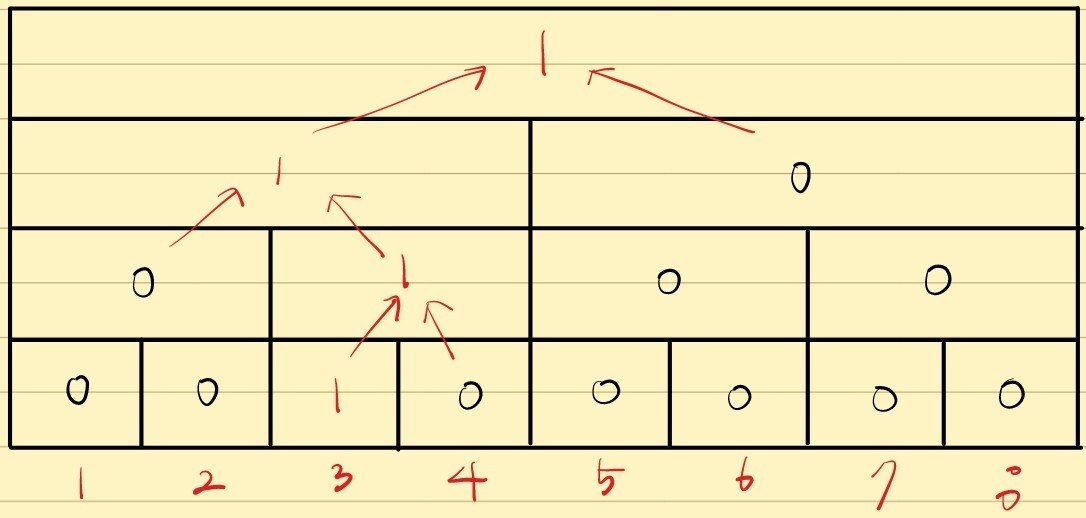
여기에 7을 넣겠습니다.
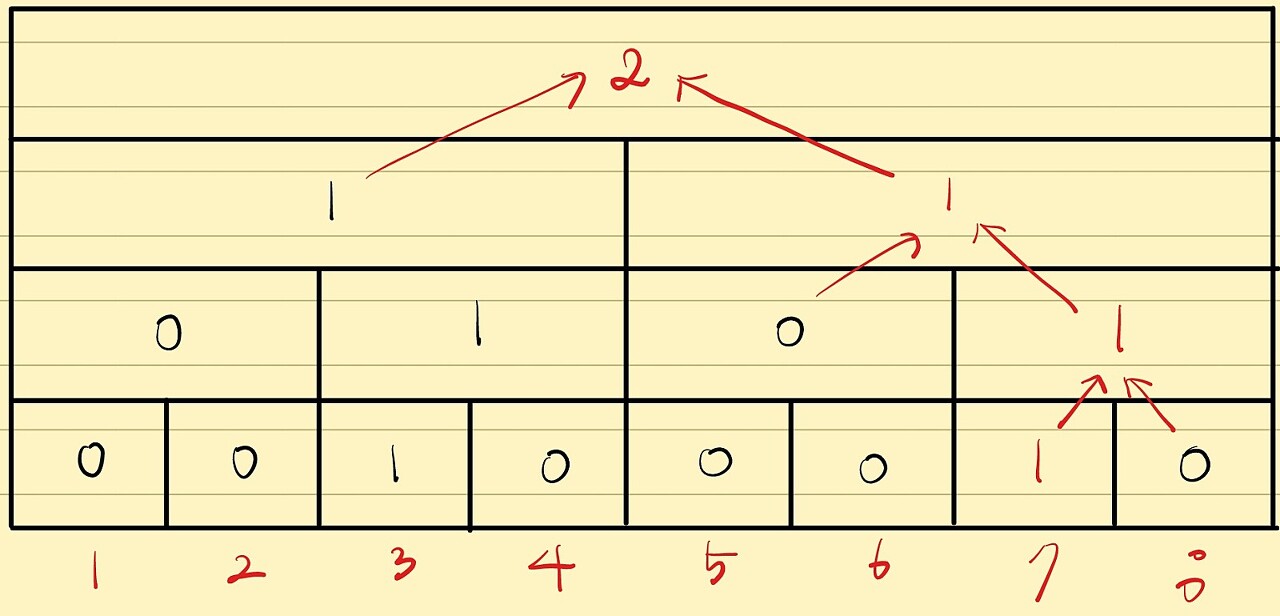
매번 구간이 이등분 되는 상황. 즉 세그먼트 트리의 루트에서 아래로 내려가는 상황을 생각합니다.
현재 구간의 왼쪽 절반의 자료의 갯수가 K개 보다 작거나 같다면 K번째 원소는 왼쪽 절반에 존재할 것입니다.
따라서 왼쪽 구간의 K번째 원소를 구하는 것으로 문제를 축소합니다.
반대로 K개 보다 많다면, K번째 원소는 오른쪽 절반에 존재할 것입니다.
왼쪽 구간의 갯수를 Diff라고 한다면 오른쪽 구간의 K-Diff 번째 원소를 구하는 문제로 축소할 수 있습니다.
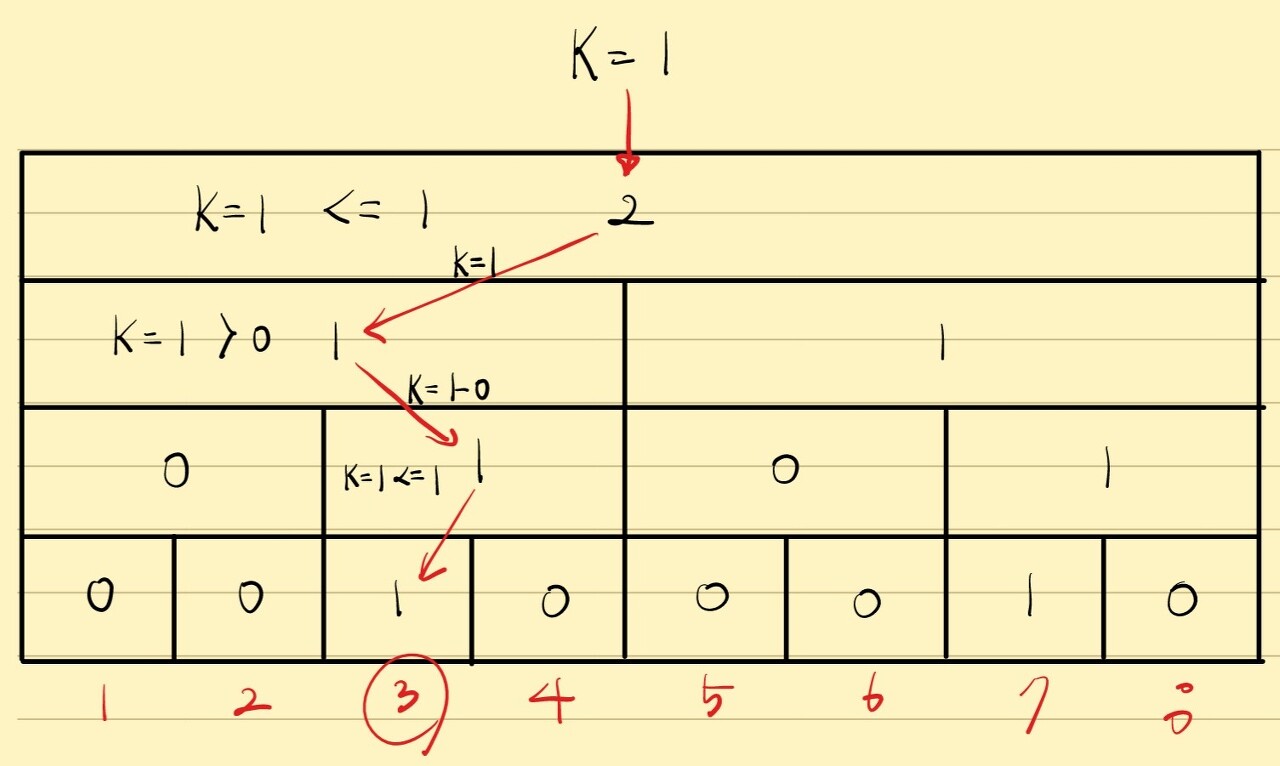
이와 같이 의사결정을 YES/NO로 진행하며 내려가고,
리프노드까지 내려가면, 해당 리프노드의 구간이 곧 K번째 수가 됩니다.
아래는 위 그림에서 1번째 원소를 구하는 과정을 보여줍니다.
이제 가운데를 말해요로 넘어갑시다.
해당 문제는 1개씩 자료를 넣어주면서 매번 중앙값을 구해야합니다.
N개의 자료를 넣어주었다면, N/2번재 원소를 구해주면 되겠죠?
즉, 세그먼트 트리로 이를 해결할 수 있는 것입니다.
아래에 정답 코드를 첨부합니다.
http://boj.kr/6d7501dcb42c4f6fb0bcc6cc95ce230f
하지만 세그먼트 트리를 활용한 Orderstatic Tree는
좋은 시간복잡도가 보장됨에도 치명적인 단점이 있습니다.
메모리가 숫자의 범위에 크게 의존한다는 것입니다. 다음의 문제를 볼까요?
[이중 우선순위큐]
https://www.acmicpc.net/problem/7662
기본적으로 우선순위큐 문제지만,
우선순위큐가 할 수 있는 모든 것은 사실 이진 검색트리가 행할 수 있습니다.
심지어 이진 검색 트리는 최솟값, 최댓값, k번째 값을 모두 O(logN)에 뽑아내는 것이 가능한 멀티플레이어입니다.
(하지만 우선순위큐를 이용하는 이유는 제한적 기능에 대해 성능이 뛰어나기 때문입니다.)
마찬가지로 세그먼트 트리를 활용한 Orderstatic Tree도 해결할 수 있죠.
최댓값은 전체 갯수가 N개라면 N번째 원소를, 최솟값은 1번째 원소를 출력하면 됩니다.
근데 범위를 한번 볼까요? 어.. int 전범위..?
대략 -20억 ~ 20억입니다. 세그먼트 트리 단원에서 말씀드렸듯이, 노드는 최소 2배의 갯수가 필요합니다.
80억개의 노드를 만드는 것은 메모리적으로도, 시간적으로도 불가능합니다.
이 문제를 어떻게 세그먼트 트리로 해결할 수 있을까요?
범위가 너무 크기 때문에, 사용하지도 않을 노드가 너무 많이 만들어지는게 문제입니다.
하지만 자료의 갯수는 1000000개 이하로 많지 않습니다.
그렇다면 자료의 크기 순서대로 1~1000000번까지 번호를 부여하는 건 어떨까요?
이것이 바로 "좌표 압축" 이라는 테크닉입니다.
좌표 압축을 위해, 데이터가 들어올 때마다 연산을 수행하는 것이 아니라 보관만 하겠습니다.
특히 삽입하는 연산의 숫자는 따로 리스트를 만들어 보관하겠습니다.
만약
I -1000
I -10000
I -1000000
I 200000
I 30000이 들어왔다고 해봅시다.
숫자만 따로 리스트에 넣어줍니다.
[-1000, -10000, -1000000, 200000, 30000]정렬해주고 번호를 부여해줍니다.
부여된 번호대로 위 연산을 바꿔줍시다.
[-1000000 : 0, -10000 : 1, -1000 : 2, 30000 : 3, 200000 : 4]만들어야하는 세그먼트 트리의 범위가 1200000만개에서 5개로 바뀌었습니다.
이제 모든 연산을 수행하고 남은 최댓값과 최솟값의 번호를 구하여, 이것을 원래 숫자로 변환해주면 됩니다.
정답 코드를 첨부합니다.
http://boj.kr/614a192d0c0c4a7c88fd2b08aa63de56
일반적인 경우 우선순위큐를 이용하게 되지만,
세그먼트 트리를 능숙하게 구현할 수 있다면, 문제를 간단하게 해결할 수 있습니다.
무엇보다 O(logN)이라는 미친 성능의 속도가 보장되어있기도 하죠.
구현 난이도가 조금 있어도, 머리로 다른 풀이 생각하는 것보다 손으로 쓰는 속도가 더 빠릅니다.
연습문제를 몇 개 투척합니다.
[중앙값 구하기]
https://www.acmicpc.net/problem/2696
[중앙값]
https://www.acmicpc.net/problem/1572
[최솟값 찾기]
https://www.acmicpc.net/problem/11003
피드백 및 오류 지적은 언제나 환영입니다.
질문은 댓글로 해주셔도 되고, 제 유튜브 채널을 방문해서 하셔도 되고, 오픈채팅방으로 하셔도 됩니다.
[유튜브 : 승욱은] 승욱은 - YouTube
[ 1:1 오픈채팅방] 카카오톡 오픈채팅 (kakao.com)
'알고리즘 설명' 카테고리의 다른 글
| [PS를 위한 자료구조 8강] 펜윅 트리의 개념과 구현 (Orderstatic Tree) (0) | 2022.03.24 |
|---|---|
| [PS를 위한 자료구조 7강] 세그먼트 트리의 응용 (금광 세그) (3) | 2022.03.24 |
| [PS를 위한 자료구조 5강] 세그먼트 트리의 구현(비재귀) (0) | 2022.03.24 |
| [PS를 위한 자료구조 4강] 게으른 세그먼트 트리의 구현 (0) | 2022.03.24 |
| [PS를 위한 자료구조 3강] 세그먼트 트리의 구현(재귀) 2 (1) | 2022.03.24 |




댓글